Trig - Finding unknown angles

So previously we have looked at using trigonometry to find unknown sides, but now we are going to be using trigonometry to find unknown angles.

Before we begin, we need to familiarise ourselves with a new type of trig ratio. We are already familiar with sin, cos, and tan. These are great for finding an unknown side length, but when the unknown is an angle, we need to use something different. For example, if we are asked to find Ө when:

sin Ө = 0.7432

To solve this we want Ө on one side of the equals sign and everything else on the other side. We have an issue, because we have sin with our Ө on one side of the equals sign. To move sin to the other side of the the equals sign, we can shift it over after we turn it into what we call "inverse sin" (which basically means "the opposite of sin"). This looks like sin^-1

So when we rearrange the equation above we get: 

Ө = sin^-10.7432

Which we can put in our calculators and solve. To put sin^-1 into your calculator, you usually just have to press the shift button on your calculator and then press the sin button. Some calculators may not have a shift button. These usually have a button that says "2nd-Func". Press this and then press the sin button. If your calculator has neither of these, your best bet would be to check an instruction manual or do a Google search by simply typing in your calculator brand and model number then "inverse sin". 

Now in this explanation I have only talked about sin, however the same applies for cos and tan. They both have inverses which are cos^-1 and tan^-1

Now we will look at some applications for these. We will often be faced with problems like the following: 

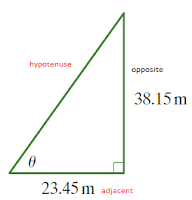
Find the unknown angle in the following triangle

 Now we deal in these in the same way we looked at when we were finding the unknown sides, by following the 5 steps.
So step 1 was to label the sides:

Step 2 was to find which sides we will be using. We are given values for our adjacent and opposite sides, so we will be using these. 

Step 3 was to work out which trig ratio we will be using. For this problem we will be using tan as that is the only one that uses the opposite and adjacent sides. 

Step 4 was to write and equation. This is where it gets slightly different to when we found the side lengths. 

We are trying to find the angle Ө, so to start with we have:

tan Ө = "something" 

To work out what this "something" is, we need to use those formula triangles we used when we were finding our side lengths. For this problem we will use this one: 

Now, we are trying to find tan Ө, we can cover up the T. By doing this we can find our "something". Covering it up we get: 

This means our something is "O over A" or basically opposite divided by adjacent. So we get:

tan Ө = O/A

Now we don't actually want tan Ө, all we want is Ө. So using the skills from the top of this post, we can rearrange our formula so it just has Ө on one side of the equals sign, and everything else on the other side. We get:

                                                                      Ө = tan^-1 O/A

Now step 5 is just substituting in values for O and A and solving for Ө. So if we look back up at the orginal question and substitute these values in we get: 

                                                                 Ө = tan^-1 38.15/23.45

If we put this in our calculators we should get and answer of 58.42..... degrees. Now if your calculator doesn't automatically put brackets in after you press the sin, cos or tan button, you will have to do this manually, so you do need brackets around the 38.15/23.45 

These skills should allow you to finish off the worksheet for trigonometry in the worksheets tab. As always, if you have any questions don't hesitate to see me or to comment on this post.