Assignment

We started an assignment on measurement in class on Monday. You will have all of Wednesday's class (25th of November) to work through this as well. It will be due at the start of the lesson on Friday the 27th of November.

I have put the assignment up in the "Assignments" tab.

If you have any questions, feel free to comment on this post, or email or chat to me in person.

Volumes of Complex Shapes

We are now spending some time looking at the volumes of complex shapes. These are shapes that do not have a constant profile through them. The shapes we are looking at will be pyramids, cones, and spheres.

Pyramids
The volume of a pyramid can be found using the following formula;

An example of using this would be; 

Cone

The volume of a cone can be found using the following formula; 

An example of using this would be; 

Sphere

The volume of a sphere can be found using the following formula; 

An example of using this would be; 

So these formula's are quite easy to use (as you can see from the examples above). With the cones and pyramids, if you do not know a dimension that you may need for the problem (i.e. the height of the shape) you will need to use Pythagoras' Theorem to work that out. If you do not remember how to do this, have a look back at some previous posts because it is used a lot in some of those. 

You should now be able to finish the worksheet on the surface area and volumes of complex shape. There will be a test soon, but I will keep you posted on that. 

As always, feel free to comment on this post if you have any questions, or email or chat to me in person. 

Surface Area of a Sphere

The following picture shows how we find the surface area of a sphere. It is just a simple formula that we can substitute values into. 

So as you can see, the only piece of information we need is the radius of the sphere. So looking at the following example, this is the working out we need for finding the surface area of a sphere. 

So finding the surface area of a sphere is really quite simple. You should now be able to finish off all of the surface area work from the second worksheet. This worksheet can be found in the "Worksheets" tab up the top of this page. 

As always, if you have any questions on this topic feel free to comment on this post, or email or chat to me in person. 

Surface Area of Cones

Today we had a look at the surface area of a cone. This can be broken into two parts;

1. The area of the circular base. 
2. The area of the curved and sloped section. 

The following diagram breaks these two pieces down and shows the formula for finding the area of each, then adds these together to come up with the total surface area of the cone. 

So what this formula shows is that all you need to find the surface area of a cone is the radius (r) and the slant height (s). So for example, the surface area of the following cone (assuming the measurements are in cm) would be found like; 

You should new be able to do most if the work on the 3rd page of the second worksheet on measurement. Work through this at home. 

If you do have any questions on the topic, feel free to comment on this post, or email or chat to me in person. 

Surface Area of a Pyramid

Today we spent some time looking at the surface areas of pyramids. We already have the skills required to find the surface area of these shapes, but I will go through an example to re-enforce the ideas.
Firstly, we need to remember that the pyramids we look at are all square pyramids. This means that the base is a square, and all 4 of the triangular faces are identical.

Before we look at an example, we should familiarise ourselves with some terms we use when talking about pyramids. The following image shows the parts of the pyramid that we need to know about:

Now when we are looking at finding the surface area, we need to find the area of the 4 identical triangular faces as well as the area of the square base. The area of a triangle is:

The "b" stands for the base length, and the "h" stands for the height of the triangle. Now for these triangular faces, the base length will be the length of one of the sides of the square base. The height of each triangle will be the slant height. 

So now, looking at an example, if we needed to find the surface area of the following pyramid; 

So to find the area of the triangular faces of this, we need the base length and the slant height. We know the base length (10cm), but we don't know the slant height. We can find this using Pythagoras' Theorem. We can make a right angled triangle using the height of the pyramid and half the base length, and use this to find the slant height. The triangle would look like so; 

Now the base of this triangle is 5cm because we are only using half of the 10cm base length to make this triangle. 

To find the slant height, we use Pythagoras' Theorem like so; 

So we now know that the slant height is 13cm. We can use this to find the area of the triangular faces of the pyramid. 

We would do this like so; 

Now we cannot forget about the square base piece either. We would find the area of this like so; 

Now the total surface area is found by adding these two areas together, giving us;

Total Surface Area = 260 + 100

Total Surface Area = 360 cm squared

Using this example, you should be able to work through the surface area of a pyramid problems on the worksheet. This worksheet can be found in the "Work Sheets" tab. 

As always, if you have any questions feel free to comment on this post, or email or chat to me in person. 

Introduction to Complex Shapes

We are now moving on from basic prisms to complex prisms and shapes. Complex prisms are prisms that do not have a constant profile through them. The complex shapes we will be looking at are cones, pyramids, and spheres.

Before we find surface areas and volumes, we need to know how to find essential information about these shapes. When dealing with cones and pyramids, we need to know how to find the slant height, the height, and also information about the base (either the radius of the base in the case of a cone, or the dimensions of the base in the case of a pyramid).

To find this information, we need to use Pythagoras' Theorem.

For example, we may have a cone like this;

We know the height, and we also know the radius of the base, but we don't know the slant height. We can use Pythagoras' Theorem to find this. Remember that Pythagoras' Theorem is; 

We need to remember that the value for "c" is always the length of the longest side of the triangle. "a" and "b" are the lengths of the other two sides. 

So going back to our cone above, we can make a right angled triangle using the height and the radius to find the slant height. It would look like this; 

Using Pythagoras' Theorem we can substitute in the values of 15 for "a" and 8 for "b" and use this to solve for the unknown side like so; 

So we have now found that the slant height is 17cm.

We can use Pythagoras' Theorem and a similar method to find out the height of the cone or the radius of the cone as well if either of these are unknown. 

If you are still struggling with using Pythagoras' Theorem, have a look at this website; 

http://www.mathsisfun.com/pythagoras.html

I have uploaded a new worksheet into the "Work Sheets" tab. You should be able to work through at least the first page of this. The second page has work on Pyramids, and the method is very much the same for these. 

If you have any questions, feel free to comment on this post, or email or chat to me in person. 

Volume of Basic Shapes

So today we looked at finding the volume of basic prisms. When I say basic prisms, what I mean are prisms that have a constant cross section. This means that the face you see on the shape is the same, no matter where you cut through the shape. For example;

The prism above has a pentagon as a face. If we were to cut a cross section at any point through this shape, it would have the same pentagon face no matter what. This works for a variety of shapes. For example; 

If a prism has this constant cross section, it is then known as a basic prism. 

To find the volume of these basic prisms we use the following formula; 

Volume = Area of Face x Height (or depth)

The face we find the area of is the face that has the constant cross section throughout the prism. For example, with the cylinder above we would find the area of the circular face, and then multiply it by the height or depth of the whole prism. 

Using this information, you should be able to make a start on the "Volume" questions on the first work sheet, which can be found in the "Work Sheets" tab. 

If you are still stuck on this topic, the following website is handy; 

http://www.mathsisfun.com/geometry/prisms.html

If you are still stuck, feel free to comment on this post, or email or chat to me in person. 

Surface Area of Cylinders

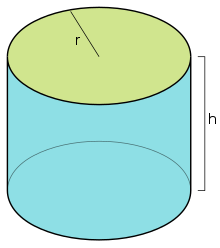
Today we looked at the total surface area of a cylinder. A cylinder looks like this:

The two pieces of information we need to find the total surface area of a cylinder are the radius (marked with an "r" on the diagram above) and the height of the cylinder (marked with a "h" on the diagram above). Remember, the radius is only half way across the circle, so if you are told the full distance across the circle you will need to half this. 

To find the surface area, imagine this cylinder all folded out as a flat 2D shape. We call this a net. The net of a cylinder looks like this: 

From this we can see that a cylinder is simply 2 circles and a rectangle. We know how to find the area of both of these. We know the area of a circle is: 

We have two of these circles, so the total area of the two circles is two lots of this, or:

Now we need to find the area of the rectangle part. For the area of a rectangle, we need the length and the width. We already know the length. This is the height of the cylinder (marked "h" on our cylinder and the net of the cylinder). We now need to find the width of this rectangle. If you look carefully you will see that the width is actually the same as the distance around the outside of the circle. This is known as the circumference of a circle. The formula for finding this is simply: 

So this is our width, and we know that the height of our rectangle is its length, so the total area of the rectangle can be found by multiplying these two together. We get:

So finally, to get the total surface area of the cylinder we combine the area of this rectangle by the area of the two circular pieces. This gives us a final formula of;

We can use this now to easily find the surface area of a cylinder. All we need to do is substitute the length of the radius (r) and the height of our cylinder (h) into this formula and use your calculator to get an answer for the total surface area. 

You should now be able to finish off most of the work from the surface area section of the worksheet. You can find a copy of this worksheet in the "Worksheets" tab. It is the first worksheet on surface area and volume. 

If you have any questions about this feel free to comment on this post, or email or chat to me in person. 

Pythagoras' Theorem

Last lesson we looked at using Pythagoras' Theorem to find unknown sides on our prisms. This is a really important skill to know and use. I did notice that a lot of students were struggling with this, or had simply forgot how to apply Pythagoras' Theorem. For today's lesson I want to look through the following document:

https://tasedu-my.sharepoint.com/personal/adam_van_sant_education_tas_gov_au/_layouts/15/WopiFrame.aspx?sourcedoc={C47B44FA-187B-45E1-95A1-F3DA9FB1A297}&file=Pythagoras%20recap.docx&action=default

Work through this today. The first two pages contain some information and some instructions. The second two pages contain some questions to work through.

If you have any questions on this topic feel free to comment on this post, or email or chat to me in person.

Surface Area of Prisms - Using Pythagoras' Theorem

So we have been looking at finding the surface area of prisms. Often the diagram will give us all of the information we need to solve these problems straight away, but sometimes we need to find some for ourselves first. An example of this can be seen with the following shape:

If we are asked to find the total surface area of this shape, we can easily do this as it is made up of basic triangles and rectangles. If we look carefully though, we will see that the top rectangular face doesn't have a length for the edge touching the triangle. 

Without this length, we cannot find the area of this face, and so we cannot find the total surface area of the prism. Fortunately we do have a way to find this side length, and that is using Pythagoras' Theorem on right angled triangles. This should have been covered in grade 8 or 9, but if you need a refresher the following link is handy: 

http://www.mathsisfun.com/pythagoras.html

Now looking at this prism, we will just look at the triangular face for now:

Using Pythagoras' Theorem we can find the length of this unknown side quite easily:

Now  that we know the unknown side length, our prism now looks like this:

We now have all of the information we need to find the total surface area of this whole prism. 

If you work this out, you should get an answer of 75 square centimeters.

We may also have a prism that looks like this:

If we look carefully at this one, we can see that we don't actually know the height of the triangular face, so we cannot find the area of this face. We will again use Pythagoras' Theorem to find this height. Again, I will just focus on the triangular face:

Now Pythagoras' Theorem will only work with right angled triangles, and this triangle above is clearly not right angled. We can, however cut this triangle in half and turn it into a right angled triangle. It would then look like so:

You will notice that the base length of the triangle is now 2cm, since we have cut it in half. We can now use Pythagoras' Theorem to find our unknown side like so: 

We now know that our height of our triangular face is 3.46cm. Our original prism now looks like so:

We can now easily find the total surface area of this prism. If you work it out you should get an answer of 73.84 square centimeters. 

I have uploaded a worksheet for this topic into the "Work Sheets" tab. You should be able to complete the first question. There are 6 different prisms for you to find the surface area of. 

As always, if you have any questions on this topic feel free to comment on this post, or email or chat to me in person.